Геометрия |
Методическая копилка |
Прямые и плоскости в пространстве |
|
Занятие 1 . |
Взаимное расположение двух прямых в пространстве. |
Занятие 2 |
Признак параллельности прямой и плоскости. |
Занятие 3 |
Взаимное расположение двух плоскостей. |
Занятие 4 |
Теорема о трёх перпендикулярах. |
Занятие 5 |
Двугранный угол. Линейный угол двугранного угла. |
Многогранники |
|
Занятие 6 |
Понятие о многограннике. Правильные многогранники. |
Занятие 7 |
Прямая и правильная призма. Параллелепипед. |
Занятие 8 |
Пирамида. Усечённая пирамида. |
Занятие 9 |
Решение задач по теме "Многогранники". |
Тела и поверхности вращения |
|
Занятие 10 |
Тела и поверхности вращения |
Занятие 11 |
Цилиндр. Конус. |
Занятие 12 |
Сфера. Шар. |
Объемы тел и площади их поверхности |
|
Занятие 13 |
Объём параллелепипеда, призмы, цилиндра, пирамиды и конуса. |
Занятие 14 |
Площади поверхностей призмы, пирамиды, цилиндра и конуса. |
Занятие 15 |
Объём шара и его частей. Площадь сферы. |
Координаты и векторы. |
|
Занятие 16 |
Координаты вектора. Скалярное произведение векторов. |
Занятие 17 |
Угол между векторами. |
Занятие 18 |
Векторное произведение векторов. |
Пирамидой называется многогранник, одна из граней которого (основание) - многоугольник, остальные грани (боковые грани) - треугольники, имеющие одну общую вершину (вершину пирамиды).
Высота пирамиды - это расстояние от вершины до плоскости основания.
Пирамида называется n-угольной, если ее основание - n-угольник.
Пирамида называется правильной, если ее основание - правильный многоугольник, а вершина проецируется в центр основания.
Боковые грани правильной пирамиды - равные равнобедренные треугольники.
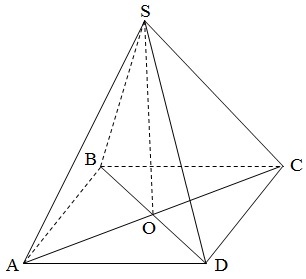 |
АВСD - основание S - вершина SO - высота АВS, ВCS, CDS, DАS - боковые грани |
2) в сечении получается многоугольник подобный основанию;
3) площади сечения и основания относятся как квадраты их расстояний от вершины.
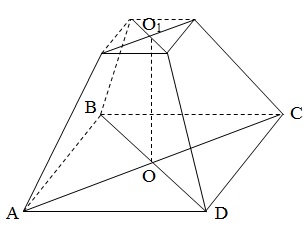
Усеченная пирамида получается из пирамиды отсечением от нее верхней части плоскостью, параллельной основанию. Основания усеченной пирамиды - подобные многоугольники, боковые грани - трапеции. Высота усеченной пирамиды - расстояние между основаниями. |
 |